We consider a spin-1 87Rb BEC, which has ferromagnetic interactions.
The initial state is prepared in the m = 0 component.
From the Bogoliubov analysis, we find that two modes are dynamically unstable
for weak interaction regime, which grow exponentially from infinitesimal noises.
The one mode has the m = 1 component with +1 vorticity and the m = -1 component
with -1 vorticity.
The other mode has the m = 1 component with -1 vorticity and the m = -1
component with +1 vorticity.
Because the complex eigenenergies of these two modes are the same, they have the
same growth rate.
Therefore, if initial noises in the m = +-1 components have angular momentum
fluctuation, it grows exponentially, i.e., the angular momentum imbalance is
amplified.
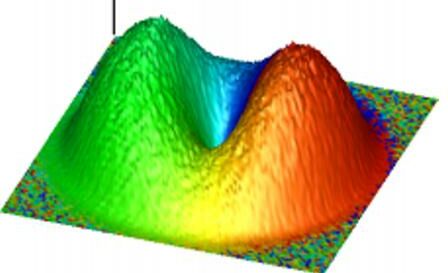(GIF, 2.8MB)
(WMV, 2.5MB)
(WMV, 284KB)
This movie shows time evolution of the m = -1 component, where initially
infinitesimal random noise is given in the m = -1 component.
The m = +1 component exhibits similar time evolution, but the circulation is
opposite to that of the movie, and hence the angular momentum conservation is
not violated.
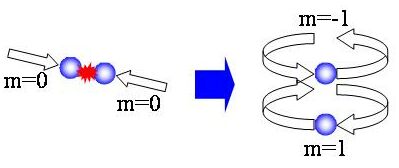
We note that this spontaneous rotation phenomenon is due to the collisions
of atoms as 0 + 0 -> 1 + (-1).
In the above example, two m = 0 atoms collide and the m = -1 atom rotates
counterclockwise and the m = 1 atom rotates clockwise.
The underlying physics is an interplay between ferromagnetic interactions and
spin conservation.
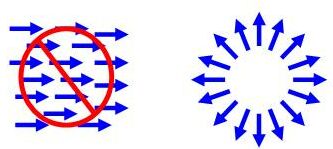
The initial state is the m=0 nonmagnetic state, and the magnetization should
occur due to the ferromagnetic interaction.
However, the uniform magnetization is prohibited because of the spin
conservation.
As a consequence, spatial spin structures is generated, which is the topological
spin texture in the present case.
The phenomenon in the above movie is triggered by the initial infinitesimal noise. That is, the initial chiral (clockwise and counterclockwise) symmetry breaking is amplified by the dynamical instability. What does occur if the initial seed has the chiral symmetry to high accuracy?
Even in this case, the chiral symmetry is spontaneously broken, and the magnetic
sublevels begin to rotate.
(GIF, 2.9MB)
(WMV, 1.7MB)
(WMV, 383KB)
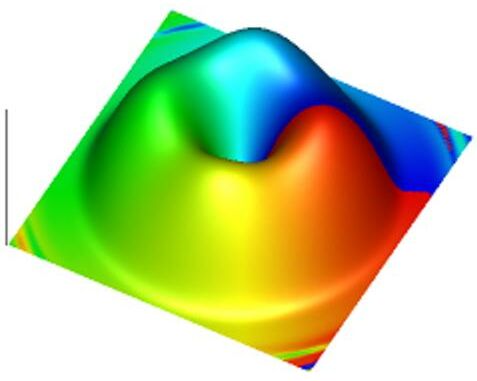
This movie shows time evolution of the m=-1 component, where the initial
infinitesimal seed has the chiral symmetry with a precision of 0.02%.
The two peaks in the first stage indicate that the clockwise and
counterclockwise rotation is mixed equally.
Subsequently, the chiral symmetry is broken, and the vortex state emerges
transiently.
In the above time evolution, the vortex state is not steady because of the
excess energy released from the initial state.
We therefore include the energy dissipation, which exists in realistic
situations.
The initial state is the same as in the above case.
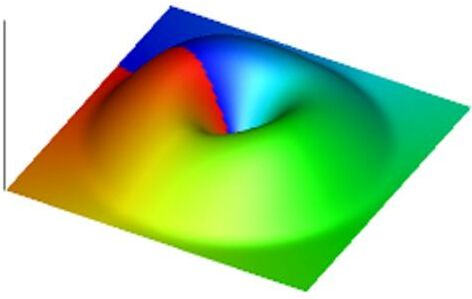(GIF, 5.8MB)
(WMV, 3.1MB)
(WMV, 595KB)
In the presence of dissipation, the system eventually goes to the topological
state.
This indicates that the state in which the chiral symmetry is broken is
energetically more favorable than the state with chiral symmetry.
Thus, the chiral symmetry breaking and the spontaneous rotation occur in the spinor BEC due to an interplay between the ferromagnetic interaction and the spin conservation.
