Dynamically stabilized bright solitons in a 2D BEC

In 1D, bright solitons can be stabilized even without a trapping potential, when the interaction is attractive. In 2D or 3D free space, however, the condensate always collapses or expands, and bright solitons are unstable.

Here we present a novel method to stabilize solitons in 2D by making the interatomic interaction oscillate rapidly using Feshbach resonance. The stabilization mechanism is similar to those of the inverted pendulum (Kapitza pendulum) with an oscillating pivot, alternating-gradient focusing, and the Paul trap.
(WMV, 407KB)

The system considered here is a BEC confined in the quasi-2D trap. We assume that the interaction is rapidly oscillated as g = g0 + g1 sin(wt) using the Feshbach resonance. The interaction is adiabatically switched on and simultaneously the radial trapping potential is turned off from t = 0 to t = 20.
Soliton stabilization
(WMV, 112KB) (GIF, 307KB)
In this movie, the right panel shows a noninteracting case for comparison.

When the adiabaticity of the ramp of the interaction and the radial trapping potential is break down, the lowest breathing mode is excited in the soliton. The frequency of the breathing oscillation is much smaller than that of the oscillating interaction.
Breathing-mode excitation
(WMV, 95KB) (GIF, 200KB)

In order to examine the interaction between solitons, we place two solitons prepared by the above method. When the relative phase between the solitons is pi, they repel each other.
Repulsive interactions between solitons
(WMV, 77KB) (GIF, 373KB)
Here weak radial trapping potential is present and the two solitons oscillate.

On the other hand, when two solitons have the same phase, they merge into one condensate.
Attractive interactions between solitons
(WMV, 77KB) (GIF, 342KB)

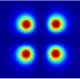
The repulsive interaction between solitons implies that possibility of soliton "lattice" formation. We then examine stabilities of four solitons, where the relative phase between adjacent solitons is taken to be pi.
Instability of "soliton lattice"
(WMV, 426KB) (GIF, 698KB)
We found that the soliton lattice is dynamically unstable.

However, if we insert a potential barrier at the center of the four solitons, they become stable.
Stability of "soliton lattice" (WMV, 78KB) (GIF, 698KB)
Thus, the soliton lattice may be formed if we put optical plugs between diagonal solitons.

BACK