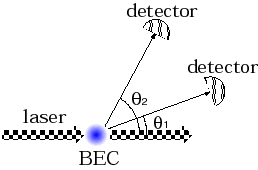
BEC に微弱で非共鳴なレーザーを照射し、 散乱される一連の光子を複数の検出器で検出するという状況を考える(上図)。 光子散乱によって BEC は擾乱を受け、それが後続の光子散乱に影響を及ぼすこと により散乱された光子対の間に相関が形成される。
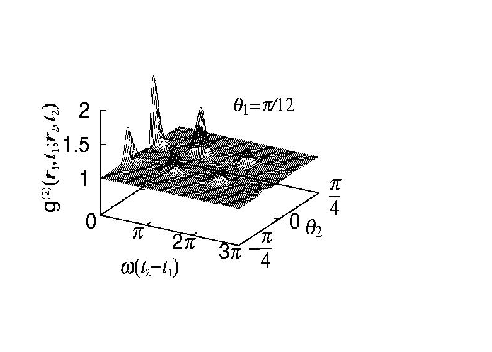
ここで散乱光の強度相関 $g^{(2)}(\theta_1, t_1;$ $\theta_2, t_2)$ を考える。 $\theta_1, \theta_2$ はそれぞれの光子の散乱角、$t_1, t_2$ は散乱時 刻を表わす。 右図は $10^3$ 個の Na 原子が凝縮している場合の散乱 光子の強度相関を表わしており、 二つのピークが減衰しながら周期的に現れていることがわかる。 二つのピークはそれぞれ光子対が同一方向 $(\theta_1 = \theta_2)$ もしくはレー ザーの進行方向に関して対称な方向 $(\theta_1 = -\theta_2)$ に散乱されやすい ということを示している。 周期はトラップ中の原子振動の半周期 $\pi\omega^{-1}$ に一致しており、減衰は 原子間相互作用の効果による。 以上のような相関は、凝縮相の存在と原子のボーズ統計性を反映したものであり、 BEC 特有の光学応答として実験的に観測されることが期待される。
戻る