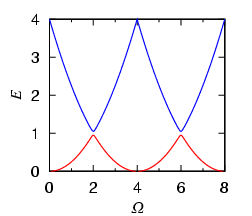
Fig. 1: The first and second energy levels for the 1D ring system.
We point out that the Bloch band picture is very suitable to describe a Bose-Einstein condensate (BEC) in a 1D ring. The ring geometry is periodic in the sense that some potential that breaks axisymmetry always has 2 pi periodicity. In this case, one finds that the rotation frequency (Omega) of the ring corresponds to the quasimomentum. As shown in Fig. 1, the energy levels certainly have the Bloch band structure.


Now, we consider a quasi-2D BEC in a harmonic-plus-quartic potential with a rotating stirrer. When the stirring frequency (Omega) is larger than the frequency of the harmonic trap, this system can be approximated by the quasi-1D ring, because the quartic confinement and the centrifugal potential produces a Mexican-hat shaped potential, and the minimum of the potential traces a quasi-1D toroidal geometry. In fact, the structure of the energy levels of this system, shown in Fig. 3, is very similar to Fig. 2. Thus, we can say that the vortex nucleation occurs due to the Bragg reflection.
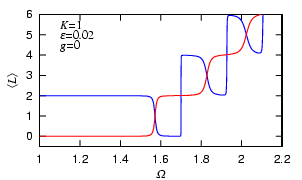
Figure 3 suggests that if we prepare the nonvortex state, switch on the rotating stirrer at low frequency, and adiabatically increase the stirring frequency, we obtain the vortex state following the first Bloch band (red curve).

Interestingly, we can also nucleate vortices by decreasing Omega following the second Bloch band (blue curve).
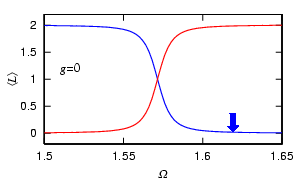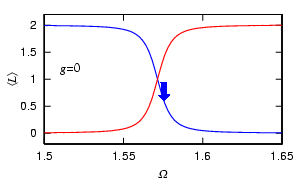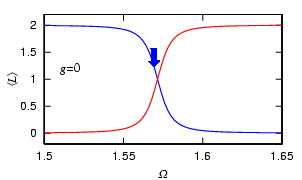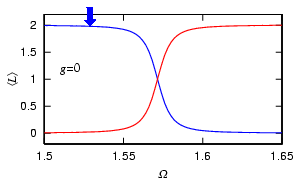
We have considered so far the noninteracting atoms. If we change the strength of interaction g using the Feshbach resonance, the frequency Omega at which the Bragg reflection occurs is shifted. Using this shift, we can adiabatically nucleate vortices by changing the strength of interaction, which may be called "Feshbach-induced Bragg reflectoin."
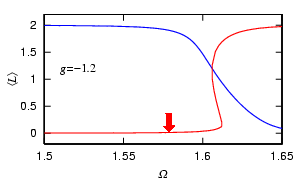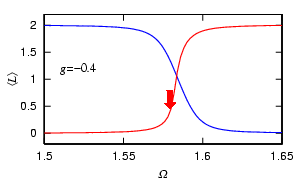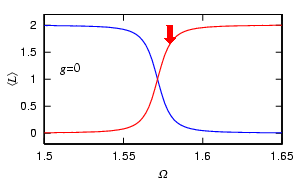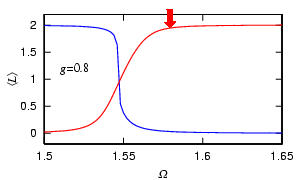

Another phenomenon peculiar to the Bloch structure is the formation of the gap soliton, in which the negative-mass dispersion counterbalances the repulsive interaction. The phenomenon analogous to the formation of the gap soliton occurs also in the present system.
When we prepare a nonvortex state, and increase the repulsive interaction at
some fixed Omega, the point at which the Bragg reflection occurs is shifted as
shown above, and vortices begin to enter the condensate (left image).
However, this state is dynamically unstable.
The instability is caused by the presence of an almost degenerate state
that is dynamically stable.
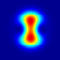
This stable state is a symmetry-broken localized state (right image), and can be
interpreted as an analogue of the gap soliton.

Thus, when we increase the repulsive interaction and arrive at the Bragg
reflection point, the condensate becomes unstable against the formation of
the gap soliton.
It is interesting to note that the localization occurs even with the repulsive
interactions.
We numerically simulated this process.
Symmetry breaking due to the emergence of the gap soliton:
(GIF, 126KB)
(WMV, 22KB)